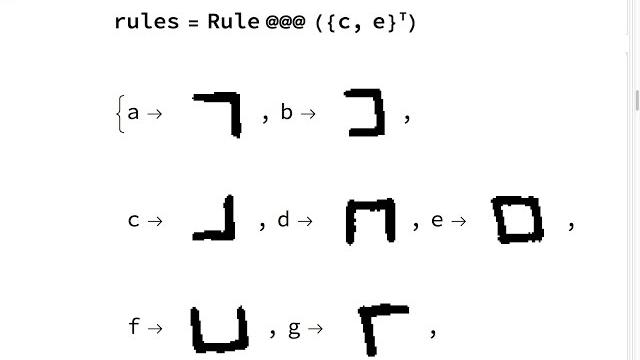Projects
Grumpy Justin's Ruby Tutorial ¶
The Ruby programming language has some weird quirks. This tutorial describes what an experienced programmer needs to know to get up-to-speed.
Shortest-path grocery shopping ¶
What’s the shortest path through my grocery store that gets all the items on my shopping list? We apply Mathematica’s powerful image-processing and graph-search algorithms to a real map of my local grocery store to figure it out.
Typesetting "The Metropolitan Man" ¶
A shell script to download and typeset The Metropolitan Man, the rationalist Superman fanfic by Alexander Wales. Armed with the PDF and the associated cover art, you can print your own hard-copy of The Metropolitan Man at online book-printing sites like lulu.com.
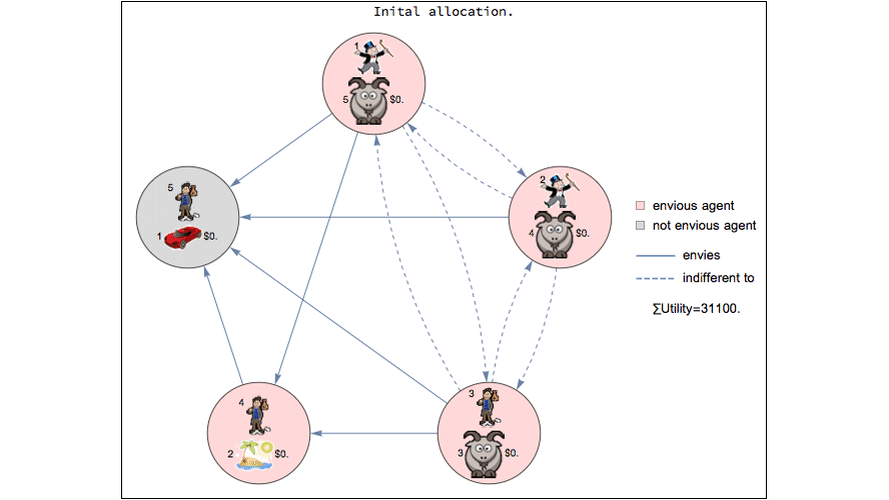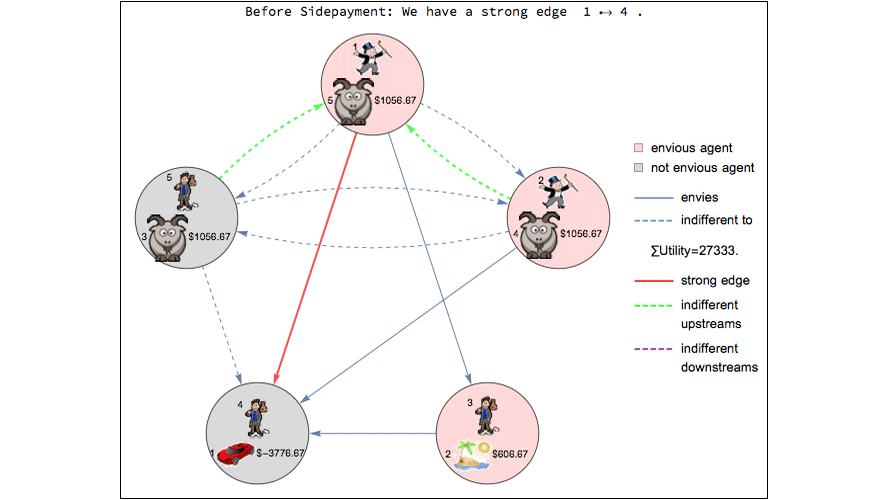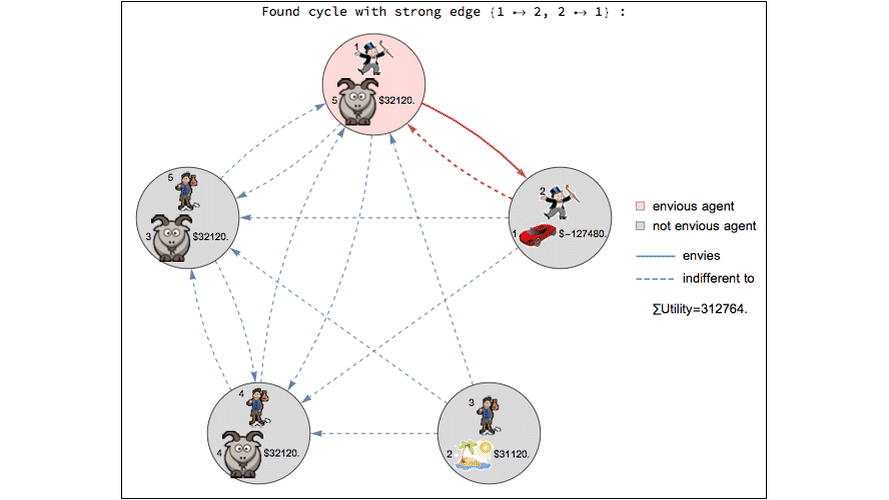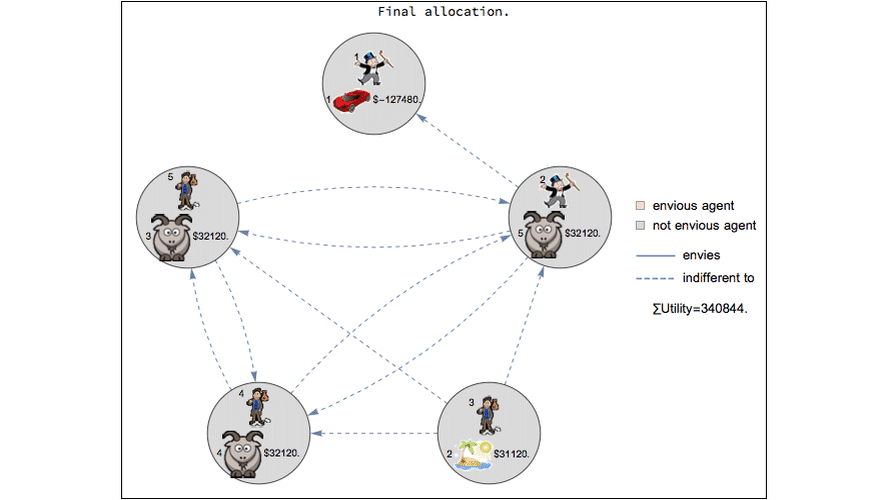
Envy-free object allocation ¶
This code illustrates an algorithm from an Dutch economics paper about object allocation. Consider the problem of allocating n objects to n people. Typically folks with crappy objects would envy the folks with desirable objects. But what if winners of the nice objects paid money to the folks who won the crappy objects? The paper presents an algorithm for figuring out how much money would need to be transferred so that no one envies anyone else.
The Smile Machine ¶
Take “stare-down” to the 21st century. Each player wears a helmet that watches the face of the wearer. When the wearer smiles, it pops a water balloon on their head. John and I developed this for Appfolio Hack Day in 2017.
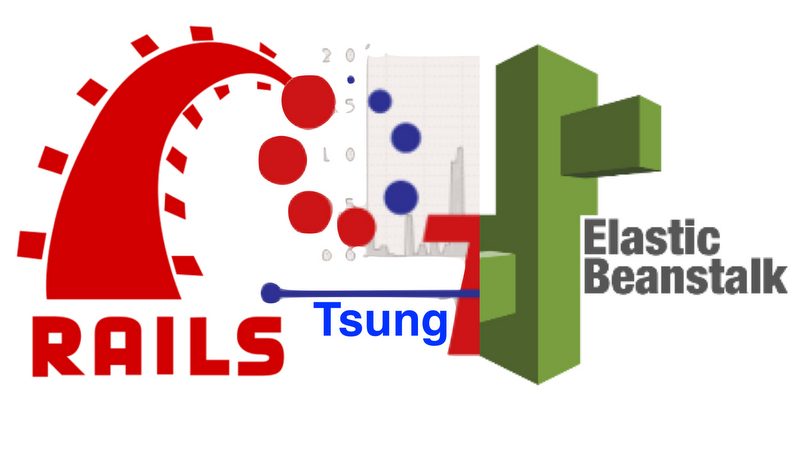
Load-testing a Rails app on AWS Elastic Beanstalk ¶
We deploy a Ruby-on-Rails app to Amazon Web Services “Elastic Beanstalk” and load-test it with Tsung. The report and presentation each describe how we used concepts from our university course – Scalable Internet Services – to scale up our web app to accommodate lots of concurrent users. The video tutorial shows how to configure Elastic Beanstalk and Tsung.
MapReduce / Paxos class project ¶
This project implements the MapReduce parallel computing algorithm and the Multi-Paxos distributed consensus algorithm. The code uses MapReduce to parallelize the computation of a word tally of several large text files; then it uses Multi-Paxos to distribute those tallies among two other computers in the form of a replicated log. The code runs on the Eucalyptus Cloud Computing infrastructure (similar to AWS).
Musical chord progression analysis ¶
The [Em,C,G,D] chord progression spans musical genres in its popularity and use. In this project, we analyze the songs on a tempo/pitch plot and explore several song mash-ups.
IR camera, frying pans, and Mathematica ¶
Comparing frying pans with an infrared camera and Mathematica.
Where's this signpost? A geodesy odyssey with Mathematica ¶
You’ve probably seen those signposts with arrows like “200 miles to LA”, “ 1200 miles to NY”, etc. Given such a sign, can you find your position on Earth?
Counting crows in a video ¶
We explore computational techniques for enumerating birds in a video file. The video was filmed in November 2011 in Simi Valley, California, and features thousands of crows on their daily evening commute from the city to a large green open space. We determine about 1200 crows fly by in 8 minutes.
Mathematica: Sunset behind the UCSB Oil Rig ¶
We use Mathematica to dynamically map out where you’d have to stand to see the sun set behind the offshore oil rig near the UCSB campus, as a function of the time of year.
Puppy or Bagel? ¶
Can Mathematica’s image classifier tell the difference between a puppy and a bagel?
Reading an analog dial ¶
Could a computer read an analog dial by processing a picture of it? We compare Mathematica’s built-in machine learning algorithms to old-fashioned image processing techniques to read the analog dial on my gas meter.
Art of Science ¶
My information-theory-based entry into the 2015 Art of Science competition run by UCSB’s Center for Science and Engineering Partnerships.
more...
We stream movies, send pictures to friends, and video-chat with distant loved ones, all digitally, and all without a second thought. Empowering this revolution behind the scenes is Information Theory, which provides a mathematical framework to quantify, compress, and transmit information. This picture illustrates an important theorem in Information Theory: the Asymptotic Equipartition Property. It formalizes and generalizes the intuitive notion that if you flip a fair coin many times, you would expect about 50% heads. In the image, each square represents a string of coinflips (with 0=tails and 1=heads), with smaller squares representing longer strings of flips. Like a family tree, each square recursively generates 4 squares below it by appending one of 4 suffixes: 00, 01, 10, or 11. Each square is black, but is made transparent depending on how close to “50% heads” its corresponding string of coinflips is. We see that the vast majority of the tiny squares at the bottom are nearly 50% heads and hence transparent, allowing the underlying Swiss pasture scene to show through.
Auto-Coloring book ¶
Using Mathematica’s morphological image processing, one can color a page coloring book in about 10 seconds. If only I had this in preschool!
Pride and Prejudice Markov chain ¶
We train a discrete markov process from text from the Jane Austen novel Pride and Prejudice, with hilarious consequences.
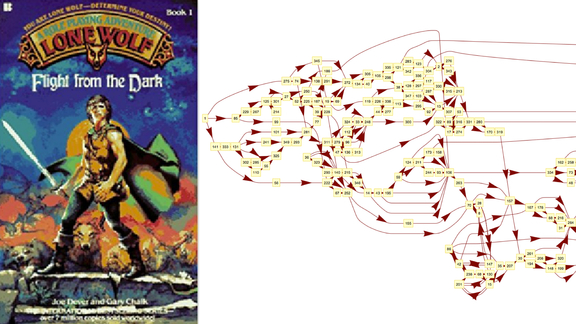
Graph analysis of a Choose-Your-Own-Adventure book ¶
We analyze Joe Denver’s classic “Lone Wolf” role-playing Choose-Your-Own-Adventure book. We find the shortest path to win and lose, and analyze the graph for cycles.
Elianscript and Mathematica ¶
Here we make a quick Mathematica program to convert strings of text to Elianscript. Then we deploy it to the Wolfram Cloud so that other folks can use our program to practice reading Elianscript.
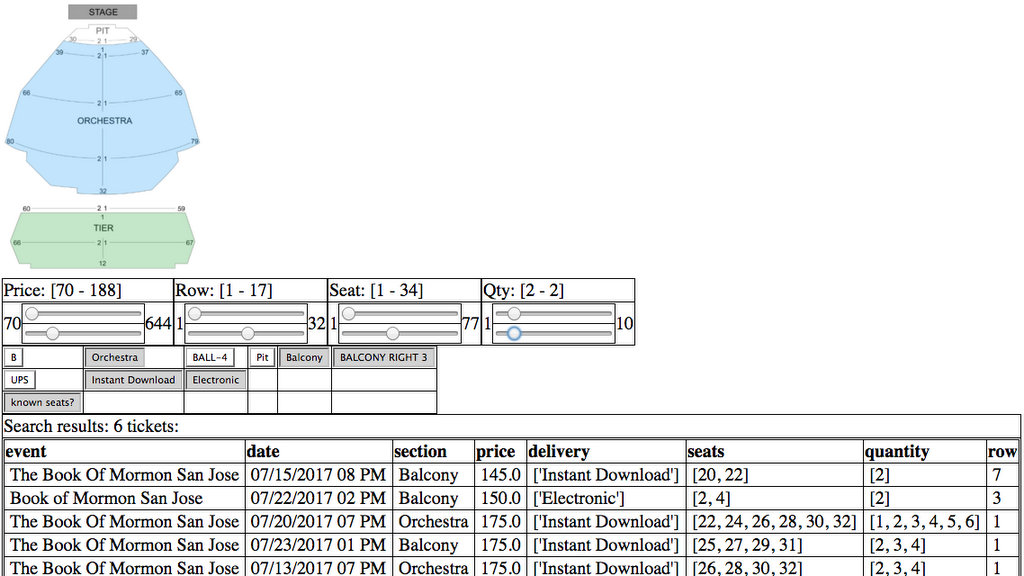
StubHub Ticket Search GUI ¶
The search capability of the StubHub online ticket marketplace sucks. So I used the browsergui browser-based GUI framework and BeautifulSoup to download, parse, and display a search interface that allows users to search across multiple events for specific sections, rows, and seats.
Counting coins in the dark ¶
A bunch of coins are in a dark room. Someone tells you how many coins there are, and how many of them are Heads. You’re allowed to flip coins over. How can you make 2 piles of coins, each with the same number of Heads?
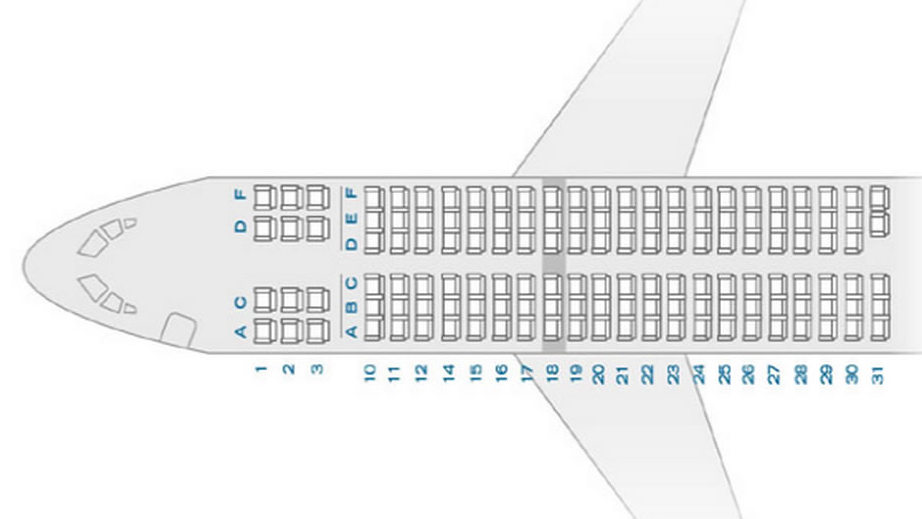
Boarding a plane ¶
100 passengers board a 100-seat airplane. They all have assigned seats, but the first passenger on board instead selects a seat at random. Each subsequent passenger tries to sit in their assigned seat, but if it’s occupied they’ll pick a seat at random. What’s the probability the last passenger sits in his assigned seat?
Lemmings ¶
One hundred lemmings are spaced 1-meter apart on a 101-meter plank in the water. You pick the initial direction of each lemming; each moves at 1m/s until it hits another lemming, at which point they each reverse direction. When all the lemmings are in the water, the game is over. Choose the initial directions of the lemmings to make the game last as long as possible (at least one lemming still on the plank).
Borwein Integrals ¶
Integrating sin(x)/x from 0 to Inf yields π/2. Same with sin(x)/x * sin(x/3)/(x/3) and sin(x)/x * sin(x/3)/(x/3) * sin(x/5)/(x/5). Continuing the pattern, the first 7 terms in this sequence all have the value π/2. However, sin(x)/x * ... * sin(x/15)/(x/15) breaks the pattern. Why?